刘徽生平简介：中国古代数学的奠基人

刘徽是魏晋时期的数学家，虽然他比赵爽（勾股弦图的发明者）晚出生了四十几年，但是他的成就在我国数学史，乃至世界数学史上都是举世瞩目的。

魏末晋初，在长期独尊儒术之后，学术界思辨之风再起，以阮籍、嵇康为首的“竹林七贤”成为不拘礼法、清静无为的典型代表，他们崇尚自然，不问世事，喜好清谈或是玄谈。在这种独特的“魏晋风骨”影响下，中国的数学界也掀起了论证的风潮。经历了由混乱到大一统的变迁的刘徽，受此影响，对《九章算术》里面的一些问题与解法进行了论证与注释。

《九章算术》是《算经十书》中最重要的一本，它是由先秦至西汉的众多学者编撰所成的一部经典著作，组成方式类似西方基督教的经典著作——《圣经》。它的涉及面很广，记载了方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股等9类246个与生产、生活实践有联系的应用问题。

这样说大家可能听得不是很明白，简单解释一下，像方田、少广、商功就是现在的面积、体积等几何问题，粟米、衰分、均输就是我们现在所说的比例问题，盈不足就是现在的盈亏问题，这个在小学奥数就已经在学了，方程与勾股比较好理解，中学生应该都懂。

《九章算术》在许多方面都做出了精彩的范例和解答：如解联立方程，分数四则运算，正负数运算，几何图形的体积面积计算等，都属于世界先进之列。但因解法比较原始，缺乏必要的证明。而刘徽就是对此均作了补充证明，写成了长达10卷的《九章算术注》，并在这些证明中，显示了他在众多方面的创造性贡献。

在代数方面，他正确地提出并定义了许多数学概念，如幂（面积）、方程（线性方程组）、正负数等等。他是世界上最早提出十进小数概念的人，并用十进小数来表示无理数的立方根。在线性方程组的解法方面，他创造了比直除法更简便的互乘相消法，这与现今解法基本一致，而且他还在中国数学史上第一次提出了“不定方程问题”。他还建立了等差级数前n项和公式。

在几何方面，刘徽的主要贡献是“割圆术”的提出与“徽率”的计算。从先秦时期开始，中国古代一直是取“周三径一”（即圆周周长与直径的比率为3：1）的数值来进行有关圆的计算。但用这个数值进行计算的结果，往往误差很大。正如刘徽所说，用“周三径一”计算出来的圆周长，实际上不是圆的周长而是圆内接正六边形的周长，其数值要比实际的圆周长小得多。东汉的张衡不满足于这个结果，他从研究圆与它的外切正方形的关系着手得到圆周率。这个数值比“周三径一”要好些，但刘徽认为其计算出来的圆周长必然要大于实际的圆周长，也不精确。

一次偶然中，刘徽看到了石匠在切割石头，看着看着竟觉得十分有趣，就站在一边，细细地观察起来。刘徽看到，一块方形的石头，先由石匠切去了四个角，四角的石头瞬间就有了八个角，然后再把这八个角切去，以此类推，石匠一直在把这些角一个一个地切去，直到无角可切为止。到最后，刘徽就发现，本来呈现方形的石块，早在不知不觉中变成了一个圆滑的柱子。石匠打磨石块的事情，每天都在发生，但就是这样的一件小事，让刘徽瞬间茅塞顿开，看到了别人没有看到的事情——“无限逼近”的思想。刘徽就像石匠所做的那样，把圆不断分割，终于发明了“割圆术”。

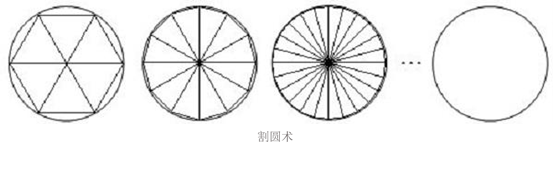
在刘徽看来，既然用“周三径一”计算出来的圆周长实际上是圆内接正六边形的周长，与圆周长相差很多；那么我们可以在圆内接正六边形把圆周等分为六条弧的基础上，再继续等分，把每段弧再分割为二，做出一个圆内接正十二边形，这个正十二边形的周长不就要比正六边形的周长更接近圆周了吗？如果把圆周再继续分割，做成一个圆内接正二十四边形，那么这个正二十四边形的周长必然又比正十二边形的周长更接近圆周。这就表明，越是把圆周分割得细，误差就越少，其内接正多边形的周长就越是接近圆周。如此不断地分割下去，一直到圆周无法再分割为止，也就是到了圆内接正多边形的边数无限多的时候，它的周长就与圆周“合体”而完全一致了。

他首先从圆内接六边形开始割圆，每次边数倍增，算到192边形的面积，得到π=157/50=3.14，又算到3072边形的面积，得到π=3927/1250=3.1416，称为“徽率”。这个结果是当时世界上圆周率计算的最精确的数据。刘徽对自己创造的这个“割圆术”新方法非常自信，把它推广到有关圆形计算的各个方面，从而使汉代以来的数学发展大大向前推进了一步。以后到了南北朝时期，祖冲之在刘徽的这一基础上继续努力，终于使圆周率精确到了小数点以后的第七位，这一成果比西方早了一千一百多年。刘徽所创立的“割圆术”新方法对中国古代数学发展的重大贡献，历史是永远不会忘记的。

刘徽还在《九章算术注》中额外加了第十章的内容，在唐朝单独出刊，后又被改名为《海岛算经》。有人指出，正是这部巨著让中国的测量学达到了巅峰，并比欧洲领先了整整一千四百年。

这本书一共有9题，主要解决高深广远之类的问题。刘徽发展了古代的“重差术”，也就是用表尺重复从不同位置观测，取所得差数，进行计算求得山高或谷深。比如《海岛算经》的第一题就是求海岛的高度：今有望海岛，立两表，齐高三丈，前后相去千步，令后表与前表参相直。从前表却行一百二十三步，人目着地取望岛峰，与表末参合。从后表却行一百二十七步，人目着地取望岛峰，亦与表末参合。问岛高及去表各几何？

翻译成现代语的意思就是，假设我们要测量一个海岛，立两根高3丈的表尺进行测量，前后相距1000步，前后两根表尺都在同一直线上,从前表尺往后走123 步，人的眼睛经过表尺末端刚好观测到岛的山顶，从后面那个表尺往后走127步，观察者的眼睛又刚好看到岛的山顶，问海岛高多少？岛与前表尺相距多远？其实这个问题就是我们现在初中数学中所学的相似三角形的应用题，解决的方法也比较简单，这里就不做展开了。

刘徽之所以能在数学上取得如此巨大的成就，主要有以下几点原因：

首先，刘徽是个富有批判精神的人。刘徽研究数学会借鉴前人之路，但不会迷信前人的定论。他批评那种墨守成规的思想，指出：“学者踵古，习其缪失。”正是这种批判精神，支持着刘徽深入研究《九章算术》，并在此基础上写出了名垂千古的《九章算术注》。

其次，刘徽是个善于发现问题本质的人。刘徽面对《九章算术》的九章264个问题，按照自己的想法给予归类，并且给出了自己的解决方式，比如：他用出入相补法来解决几何图形问题，用重差法解决各种测量问题，用今有术来解决比例问题……做到“事类相推，各有攸归。”

最后，刘徽是个善于借助工具的人。面对枯燥、空洞的数学问题，刘徽善于借用图形来解决实际问题。不论是前面的割圆术，还是在《九章算术注》记载的棋验法（即立体几何模型法），又或者是在各种几何图形涂上色，这一切都是刘徽善于借助工具，化抽象为直观的表现。

刘徽的一生是为数学刻苦探求的一生。他虽然地位低下，但人格高尚。他不是沽名钓誉的庸人，而是学而不厌的伟人，他给我们中华民族留下了宝贵的财富。而由于他在数学史上的突出贡献，也有人称他为“中国数学史上的牛顿”。